前言
通过决策表可以为多条件组合的场景设计测试用例。决策表的设计方法适用于:不同逻辑条件的组合值,分别执行不同的操作。列出全部条件桩、动作桩,填写条件项、动作项,制作初始决策表,合并决策表。
1.1 前面方法忽略的问题
前面介绍的测试用例设计方法的场景法、等价类划分、边界值分析法都忽略输入组合的问题。
测试两位数加法计算器的测试没有考虑输入组合。
1.2 决策表是什么
决策表(Decision Table)又称判断表,是分析和表达多逻辑条件下执行不同操作情况的工具,适用于测试复杂业务规则组合的场景。
优点:能够将复杂的问题按照各种可能的情况全部列举出来,简明并避免遗漏。因此,利用判定表能够设计出完整的测试用例集合。
缺点:不能表达重复执行的动作,如循环结构。
判定表不能很好的伸缩。如有n个条件的判定表有2n个规则。
在一些数据处理问题当中,某些操作的实施依赖于多个逻辑条件的组合,即:针对不同逻辑条件的组合值,分别执行不同的操作。判定表很适合于处理这类问题。
决策表的组成
条件桩(Condition Stub):列出所有可能影响结果的输入条件。
动作桩(Action Stub):列出所有可能的输出动作(结果)。
条件项(Condition Entry):每个条件的取值(如 True/False、Yes/No)。
动作项(Action Entry):对应条件下执行的动作(如通过/拒绝、计算折扣)。
规则:任何一个条件组合的特定取值及其要执行的相应操作。在判定表中贯穿条件项和动作项的一列就是一条规则。
1.3 决策表的分析步骤
有2个输入就叫有2个因素。1个输入代表1个因素。比如,输入第一个数值和输入第二个数值。每个输入有x种情况,就叫有x个水平。每个输入的值,叫水平。
(1) 需求分析;
分析输入和输出,用等价类划分分析输入的各种情况、输出的各种情况;
(2) 画判定表或决策表;
(3) 分析与简化判定表;
构造决策表的5个步骤:
(1) 确定规则的个数。有n个条件的决策表有2n 个规则(每个条件取真、假值)。
(2) 列出所有的条件桩和动作桩。
(3) 填入条件项。
(4) 填入动作项,得到初始决策表。
(5) 简化决策表,合并相似规则。
若表中有两条以上规则具有相同的动作,并且在条件项之间存在极为相似的关系,便可以合并。
合并后的条件项用符号“-”表示,说明执行的动作与该条件的取值无关,称为无关条件。
1.4 决策表案例
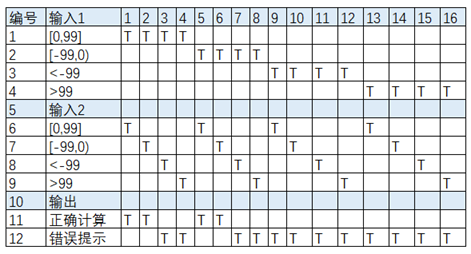
(1) 分析输入条件和输出条件
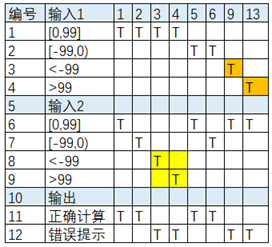
输入1:
条件1:0<=X<=99
条件2:-99<=X<0
条件3:X<-99
条件4:X>99
输入2:
条件1:0<=X<=99
条件2:-99<=X<0
条件3:X<-99
条件4:X>99
输出:
正确计算;
错误提示;
(2) 原始决策表/判定表
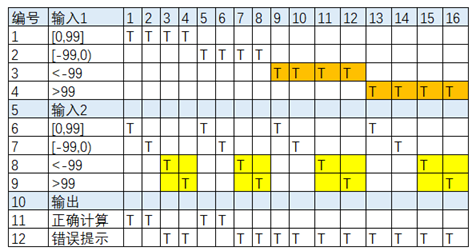
(3) 优化决策表
将错误的用颜色标注出来,保留输入1的每个错误水平,输入2的正确水平;保留输入2的每个错误水平,输入1的正确水平。
(4) 优化策略
测试基本功能的保留;正向用例;
一个输入错误,其他输入无所谓,可以整合;
所有输入都要错过;
(5) 最终的决策表
通过决策表后仍然有风险,测试难以做到100%覆盖,只能尽量科学的减少失误。决策表有多少列就可以写多少条用例。
1.5 决策表练习
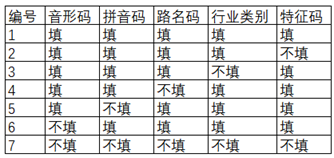
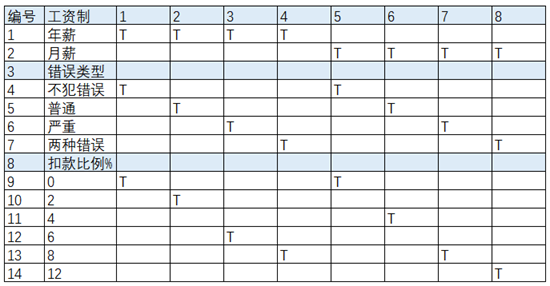
案例:某厂工资发放需求。
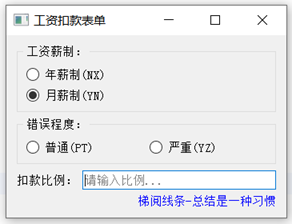
(1) 工资分为年薪制,月薪制,两者互斥;
(2) 错误程度分为普通和严重,两者可同时具备;
(3) 年薪制员工犯普通错误扣工资2%,犯严重错误扣工资6%;
(4) 月薪制员工犯普通错误扣工资4%,犯严重错误扣工资8%;
决策表:
1.6 决策表适用范围
适用于多种输入存在组合的情况。
1.7 决策表的局限性与优化策略
导致测试量暴增。

上面有5个输入条件,即5个因素,假设每个输入条件,只考虑填和不填2种情况,即2个水平,那么,决策表的测试点会有2的5次方个。水平的因素次方。
决策表优化策略
(1) 正向用例:全部都填;
(2) 均匀覆盖:每个条件的填和不填都测过,均匀的分布即可,某个条件选择反向值,比如不填,那么其他条件就选择填;
(3) 反向用例:全部不填;